Na fotografiji: Atenska šola (detajl s Platonom in Aristotelom v sredini),
Raffaello, Public domain, Wikimedia Commons

Aristotel (384–322 pr. n. št.) je bil nedvomno človek mnogih poklicev, toda ali se je ukvarjal tudi z lesom? »To pa že ne,« bi bil moj prvi odgovor. Pa vendar je Aristotel del svoje pozornosti namenil tudi lesu, tako kot mnogim materialom, ki jih je opazoval, o njih razmišljal in jih uporabljal pri svojih razlagah pojavov. Oglejmo si na kratko dva z lesom povezana mehanska pojava, o katerih je razmišljal, in jih povežimo z današnjo uporabo in razumevanjem.

Problem št. 1

Tritočkovni upogib lesa

Vsak od nas je to že počel! Verjamem, da je za taborni ogenj vsak že kdaj zlomil kos lesa – palico ali vejo. Vsi smo torej naredili nekaj, čemur pravimo tritočkovni upogib do končne obremenitve – loma. In ker vsak deluje intuitivno, je les pri tem zgrabili na njegovih koncih in ga na sredini prelomil čez koleno. Zakaj bi to počeli drugače, če je na ta način najbolj enostavno, kajne? Torej, storili smo popolnoma enako stvar, kot je tista, o kateri je razmišljal Aristotel:

»Zakaj se kos lesa iste velikosti lažje prelomi na kolenu, če ga prelomimo tako, da držimo konce lesa na enaki razdalji od kolena, kot pa če ga držimo blizu kolena? In če kdo prisloni kos lesa na tla in nanj postavi nogo, zakaj se les lažje zlomi, če se ga drži dlje od noge? Ali zato, ker je v prvem primeru središče koleno, v drugem pa stopalo, in bolj ko je predmet oddaljen od središča, lažje se ga upogiba in je tisto, kar naj bi se zlomilo, treba upogniti?«

(Mechanics, 14, str. 4443, Barnes 1984)

Problem, ki ga je opisal Aristotel, je mogoče zlahka prikazati (slika 1A) in ga pripeljati do pravilnih sklepov, da boste kos materiala pri upogibanju zlomili z najmanj sile, če ga podložite na sredini. To načelo – simetrična obremenitev pri upogibanju v treh točkah – uporabljamo pri preizkusnih materialih na univerzalnih testirnih strojih, da dobimo modul elastičnosti, upogibno trdnost, delo, mejo plastičnosti in številne druge podatke. Nastavitev simetrije obremenitve prinaša najčistejše informacije o materialu, saj so tudi momenti, ki delujejo na material, simetrični. Edini dodatni pogoj, ki ga moramo v nasprotju z lomljenjem drv izpolniti v laboratoriju, je tudi simetrična geometrija vzorcev, zato imajo naši leseni vzorci najpogosteje pravokotno obliko (slika 1B).

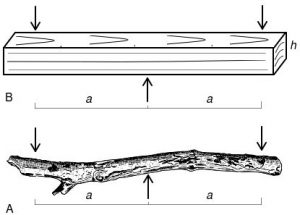
Slika 1. Preizkušanje tritočkovnega upogiba veje za taborni ogenj (A) in kosa lesa v laboratoriju (B).

Naslednji od Aristotelovih zaključkov, ki je za nas zanimiv, je razdalja med kolenom (oziroma obremenitveno glavo pri univerzalnem testirnem stroju) in rokami (oziroma podporami pri univerzalnem testirnem stroju). Ta razdalja je ključnega pomena pri upogibnem preizkusu, saj nam omogoča lomljenje materiala pri nižjih silah, brez večjih tlačnih sil, ki povzročijo odtise podpor ter glave testirnega stroja, in brez večjih strižnih napetosti. Ta razdalja se uporablja pri izračunu tako imenovanega vitkostnega količnika, razmerja med razdaljo med nosilci (2a) in višino vzorca (h), ki je predpisan v vsakem nacionalnem ali evropskem standardu za preskušanje kateregakoli materiala pri tristopenjskem upogibanju.

Problem št. 2.

Cepljenje lesa

Naslednjo stvar, ki jo je opazil Aristotel, dobro poznajo tisti, ki so kdaj pripravljali drva tako, da so večje kose s sekiro cepili v manjše. Poglejmo najprej, kaj pravi Aristotel o cepljenju lesa:

»Kako to, da se kos lesa, če nanj položite težko sekiro, nanjo pa še težko utež, ne razcepi skoraj nič, medtem ko se razcepi, če sekiro dvignete in z njo zamahnete po lesu, pa čeprav ima sekira takrat, ko les zadene z udarcem, veliko manjšo težo kot takrat, ko jo položimo na les in jo dodatno obtežimo?«

(Mechanics, 19, str. 4448, Barnes 1984)

Problem cepljenja lesa spada na področje mehanike loma, pri čemer Aristotel primerja dve situaciji: 1) težak klin, počasi nameščen na les, ki ne povzroči razcepa (slika 2A), in 2) veliko lažji klin, ki trči v les s hitrostjo in sproži razcep (slika 2B). Razlaga, zakaj drugi scenarij vodi do cepitve, je preprosta: da v lesu nastane razpoka, ki bi se nadalje širila skozenj, je potrebna določena energija (kritična energija loma). Čeprav je torej začetna teža klina veliko manjša kot v prvem primeru, kritično energijo loma zagotovi kinetična energija. Ko klin s svojim zagonom udari v les, se njegova kinetična energija na njegovi konici pretvori in zgosti v napetost, s čimer zlahka premaga kritično energijo loma in odpre razpoko, ki se nato še veliko lažje širi. Aristotel je pravilno dojel razliko med statičnim in dinamičnim vplivom klina na kos lesa, vendar je ni mogel pravilno razvozlati, ker so Newtonovi zakoni prišli veliko pozneje, v 17. stoletju.

Slika 2. Cepitev lesa s potencialno energijo (A) in kinetično energijo (B).

Sklepi

Iz navedenih Aristotelovih primerov se lahko naučimo več stvari:

• Njegove misli o upogibanju in cepljenju lesa tudi danes, okoli 2400 let pozneje, predstavljajo veljavna načela. Na teh načelih temelji več trenutnih teorij in merilnih naprav, ki nam še naprej omogočajo podrobnejše razumevanje problemov.
• Dihotomija med kinetično in potencialno energijo, ki jo ponazarja drugi primer, je še vedno vključena v naš izobraževalni sistem (kot del rednega pouku fizike), Aristotelu pa se utemeljeno pripisuje, da je njen oče (ne samo zaradi opisanega primera).
• Čeprav bi Aristotela lahko šteli ta »mrtvega avtorja«, saj ga splošna javnost ne bere veliko (in njegovo pisanje je res težko prežvečiti …), ga pri testiranju materialov v laboratoriju oziroma pri pripravi drv zlahka oživimo.
• Načelo pojavov lahko razkrijeta intuicija in besedna analiza pojavov, za globlje razumevanje pa je treba razviti teorijo na podlagi znanstvene metode.

Največji preobrat nas, tako kot pogosto v detektivskih zgodbah, čaka ravno na koncu. Kot vemo, je znanost nekakšno tekmovanje hipotez, na koncu pa odloča dokaz, katere so pravilne. Torej: obstaja hipoteza, da zgornjih stvari iz »Mehanike« morda ni napisal Aristotel, ampak Arhitas iz Taranta (410–350 pr. n. št.). Ker nisem strokovnjak za staro grščino, morate o dokazu povprašati koga drugega ali pa to ugotoviti sami.

Dr. Václav Sebera,
raziskovalec v InnoRenew CoE

Viri

– Barnes, J. (ur.). The complete works of Aristotle. The Revised Oxford Edition. 1984. Princeton University Press.

– Winter, T. N. (2007). The Mechanical Problems in the Corpus of Aristotle. Faculty Publications, Classics and Religious Studies Department. 68. https://digitalcommons.unl.edu/classicsfacpub/68